|
  |
|
|
����20�N3��1��(�y)�@�@��Z�����ƌ�����@��21����J�u��
�N�ԃe�[�}�w��͂��Ă�ׂ��͢�D������x����{���̊w�́x
���������Ɓ@�ؓc�k�O�u�r���R���Y�@�e�[�}�u�Q���~�Q���̂����Z�v���
�E�{DVD�ɂ́A�ؓc�搶�Ɛ��R�搶�̗��������Ƃƌ������c������^���Ă���܂��B
����̎��Ƃ́A�ؓc�搶�͢�Z�����ƌ����@���J�u����ł̍Ō�̌��J���ƁA���R�搶�́A�R�N�ԒS�C�����q�ǂ������Ƃ̍Ō�̌��J���Ƃł��B
�E�ؓc�搶�̂������́A���Ƃ��s�������_�̂��̂ł��B
�E���̏�����́A���j�ɍs���频��Ɛ��𑗂�q�ǂ��̏����ł��B
|
|
|
|
|
|
  |
|
|
 |
�@����
�ؓc���Z���i��36���j |
|
|
|
���J���Ƃ����^�B
���������₷���悤�ɁA45���̎��Ƃ��36���ɏk�߂ĕҏW���Ă���܂��B
|
|
|
 |
|
|
 |
�A���� ���R�搶�i��36���j |
|
|
|
���J���Ƃ����^�B
���������₷���悤�ɁA45���̎��Ƃ��36���ɏk�߂ĕҏW���Ă���܂��B |
|
|
 |
|
|
 |
�B�������c��i��55���j |
|
|
|
| ���Ǝ�2���ƃp�l���X�g�ɂ����Ɠ��e�̋��c |
|
|
|
�@�@ 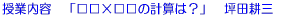 |
|
|
|
�u�����~������1213�v�̌v�Z�ɓ��Ă͂܂遠���~�������l����
���ɓ��Ă͂܂�v�Z���l����̂��Ƃ������Ƃ�`����B
���Z�̊w�K���s���Ă��Ȃ������͎��s����ŐF�X�Ȑ��������Ă͂߂čl����B
|
|
�������u1213�v�ɋ߂����̂��݂��悤�ƁA�l����i�߂�
�������݂���Ȃ��̂́u�Ȃ����v���ł��邾���l���Ă����B�B
|
|
������ς��āu�����~������1152�v�̌v�Z�ł͂ǂ������l����
�����������̂��߁A���l�Ȏ����o�ꂷ��B���������v�Z���ᖡ������A�f�����݂���H�v�������肵�āA���̒�����u�����Z�̂��܂�v�����o���Ă����B�@�@�@
|
���܂������
�������鐔��2�{�ɂȂ�Ƃ����鐔�������ɂȂ�B
�i��j36�@�~�@32�@���@1152
�@�@�@��(2�{) ��(1/2) ��(����)
�@�@�@72�@�~�@16�@���@1152
������Z�̂��܂裂������A����ɂ���ĐV���Ȍv�Z�̔����̕����Ɏv�l��i�߂�B
�i��j36�@�~�@32�@���@1152
�@�@�@�@��(1/3) ��(3�{) ��(����)
�@�@ ���� �~ ���� ���@1152 |
|
|
|
�@�@ 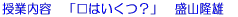 |
|
|
|
1.�Q�T�~���~�����P�O�O�@�́��ɓ��鐔���l����
�����ł́A�u�Q�T�~�S���P�O�O�v�Ƃ����P�O�O�̏�@�I�Ȍ����������邱�Ƃ��˂炢�Ƃ���B�u�Q�T�~�S�~�P�v�A�u�Q�T�~�Q�~�Q�v�A�u�Q�T�~�P�~�S�v�Ǝ����ł����Ƃ��ɁA�ǂ̎������ǂQ�T�ɂS�������邱�ƂƓ����A�Ƃ������߂�����B
|
|
2.�Q�T�~���~�����R�O�O�@�́��ɓ��鐔���l����
�Q�T�~���~�����P�O�O�@�̂Ƃ��ɍl����������ɂ��āA�Q�T�~���~�����R�O�O�@�́��ɓ��鐔���l����B�R�O�O�͂P�O�O�̂R�{������A�i�Q�T�~�S�j�~�R���R�O�O�@�Ƃ������������l������B
|
|
3.���\���ꂽ������������
���̂悤�Ȏ������\���ꂽ�B
�u�Q�T�~�S�~�R�v�u�Q�T�~�R�~�S�v�u�Q�T�~�Q�~�U�v�u�Q�T�~�U�~�Q�v
�ǂ̎����A�Q�T�ɂP�Q�������Ă���Ɖ��߂���B�܂��A�Q�T�~�S���P�O�O�@���������A�Q�T�~�S�~�R���P�O�O�~�R���R�O�O�@�Ƃ��Ă����Ɍv�Z�ł��邱�ƂɋC�Â��B
|
������傫�������́H
���Ɋ���Ă�����A��������ԑ傫���M�Z���l����B�����̏\�̈ʂ��X�ɂ��A��̈ʂ��c���������̑g�ݍ��킹�ōl���Ă����B������l���������������l���������ȒP�Ȃ��ƂɋC�Â��B |
|
|
|
 |
|
(c)Copyright2023 KIKAKUSHUDAN SOU CO., LTD. All Rights Reserved. |
|
|
 |